这里主要坦述MD5和AES的流程分析。

这两种代表了目前最主流的加密组合。

MD5

聊起md5，许多开发人员用这个的目的，做个hash值，api签名加个密，密码md5….

散列函数

散列函数，也称作哈希函数，消息摘要函数，单向函数或者杂凑函数。散列函数主要用于验证数据的完整性。通过散列函数，可以创建消息的“数字指纹”，消息接收方可以通过校验消息的哈希值来验证消息的完整性，防止消息被篡改。散列函数具有以下特性：

散列函数的运算过程是不可逆的，这个称为散列函数的单向性。
对于一个已知的消息及其散列值，要找到另外一个消息使其获得相同的散列值是不可能的，这个特性称为散列函数的弱碰撞性。这个特性可以用来防止消息伪造。
任意两个不同消息的散列值一定不同。
对原始消息长度没有限制。

任何消息经过散列函数处理后，都会产生一个唯一的散列值，这个散列值可以用来验证消息的完整性。计算消息散列值的过程被称为“消息摘要”，计算消息散列值的算法被称为消息摘要算法。常使用的消息摘要算法有：MD—消息摘要算法，SHA—安全散列算法，MAC—消息认证码算法。本文主要来了解MD算法。

MD5算法原理

假设原始消息长度是b（以bit为单位），注意这里b可以是任意长度，并不一定要是8的整数倍。计算该消息MD5值的过程如下：

1.填充信息

在计算消息的MD5值之前，首先对原始信息进行填充，这里的信息填充分为两步。
第一步，对原始信息进行填充，填充之后，要求信息的长度对512取余等于448。填充的规则如下：假设原始信息长度为b bit，那么在信息的b+1 bit位填充1，剩余的位填充0，直到信息长度对512取余为448。这里有一点需要注意，如果原始信息长度对512取余正好等于448，这种情况仍然要进行填充，很明显，在这时我们要填充的信息长度是512位，直到信息长度对512取余再次等于448。所以，填充的位数最少为1，最大为512。
第二步，填充信息长度，我们需要把原始信息长度转换成以bit为单位，然后在第一步操作的结果后面填充64bit的数据表示原始信息长度。第一步对原始信息进行填充之后，信息长度对512取余结果为448，这里再填充64bit的长度信息，整个信息恰好可以被512整除。其实从后续过程可以看到，计算MD5时，是将信息分为若干个分组进行处理的，每个信息分组的长度是512bit。

2.信息处理

在进行MD5值计算之前，我们先来做一些定义。

信息分组定义
原始信息经过填充之后，最终得到的信息长度（bit）是512的整数倍，我们先对信息进行分组，每512bit为一个分组，然后再将每个信息分组（512bit）再细分为16个小的分组，每个小分组的长度为32bit。规定如下
Mp 代表经过填充之后的信息
LM 表示Mp的长度（以bit为单位）
N 表示分组个数，N = LM/512
M[i] 表示将原始信息进行分组后的第i个信息分组，其中i=1…N
X[i] 表示将M[i]进行分组后的第i个小分组，其中i=1…16
标准幻数定义
现定义四个标准幻数如下，
A = 01 23 45 67
B = 89 ab cd ef
C = fe dc ba 98
D = 76 54 32 10
在计算机中存储时，采用小端存储方式，以A为例，A在Java中初始化的代码为为A=0x67452301
常量表T
T是一个常量表，T[i] = 4294967296 * abs(sin(i))的运算结果取整，其中i=1…64

upload successful

辅助方法

我们定义四个辅助方法。
F(x,y,z) = (x & y) | ((~x) & z)
G(x,y,z) = (x & z) | (y & (~z))
H(x,y,z) = x ^ y ^ z
I(x,y,z) = y ^ (x | (~z))
其中，x，y，z长度为32bit

下面就是最核心的信息处理过程，计算MD5的过程实际上就是轮流处理每个信息分组的过程。

    A=0x67452301
    B=0xefcdab89
    C=0x98badcfe
    D=0x10325476
    for( j=1;j<=N;j++){  //依次处理每个分组，其中N代表分组个数
      AA = A 
      BB = B 
      CC = C
      DD = D
      //开始处理分组，每个信息分组要经过4轮处理
      /*第一轮
      假设 [abcd k s i] 表示执行的运算是 a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s)，其中<<<表示循环移位。第一轮运算就是对分组执行以下所示的16次运算，运算的顺序从左到右。*/
    [ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4]
    [ABCD 4 7 5] [DABC 5 12 6] [CDAB 6 17 7] [BCDA 7 22 8]
    [ABCD 8 7 9] [DABC 9 12 10] [CDAB 10 17 11] [BCDA 11 22 12]
    [ABCD 12 7 13] [DABC 13 12 14] [CDAB 14 17 15] [BCDA 15 22 16]

    /*第二轮
    假设 [abcd k s i] 表示执行的运算是 a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s)，其中 <<<表示循环移位。第一轮运算就是对分组执行以下所示的16次运算，运算的顺 序从左到右。*/
    [ABCD 1 5 17] [DABC 6 9 18] [CDAB 11 14 19] [BCDA 0 20 20]
    [ABCD 5 5 21] [DABC 10 9 22] [CDAB 15 14 23] [BCDA 4 20 24]
    [ABCD 9 5 25] [DABC 14 9 26] [CDAB 3 14 27] [BCDA 8 20 28]
    [ABCD 13 5 29] [DABC 2 9 30] [CDAB 7 14 31] [BCDA 12 20 32]

    /*第三轮
    假设 [abcd k s i] 表示执行的运算是 a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s)，其中<<<表示循环移位。第一轮运算就是对分组执行以下所示的16次运算，运算的顺 序从左到右。*/
    [ABCD 5 4 33] [DABC 8 11 34] [CDAB 11 16 35] [BCDA 14 23 36]
    [ABCD 1 4 37] [DABC 4 11 38] [CDAB 7 16 39] [BCDA 10 23 40]
    [ABCD 13 4 41] [DABC 0 11 42] [CDAB 3 16 43] [BCDA 6 23 44]
    [ABCD 9 4 45] [DABC 12 11 46] [CDAB 15 16 47] [BCDA 2 23 48]

    /*第四轮
    假设 [abcd k s i] 表示执行的运算是 a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s)，其中<<<表示循环移位。第一轮运算就是对分组执行以下所示的16次运算，运算的顺序从左到右。*/
    [ABCD 0 6 49] [DABC 7 10 50] [CDAB 14 15 51] [BCDA 5 21 52]
    [ABCD 12 6 53] [DABC 3 10 54] [CDAB 10 15 55] [BCDA 1 21 56]
    [ABCD 8 6 57] [DABC 15 10 58] [CDAB 6 15 59] [BCDA 13 21 60]
    [ABCD 4 6 61] [DABC 11 10 62] [CDAB 2 15 63] [BCDA 9 21 64]
    
    //将当前消息分组的运算结果和上一次的结果进行累加
    A = A + AA
    B = B + BB
    C = C + CC
    D = D + DD
}
//最终我们按照低字节在前的顺序依次将A,B,C,D拼接起来，就是计算得到的MD5值，因此，MD5值的长度是固定的，为128bit。

作者：咸鱼0907
链接：https://www.jianshu.com/p/93a8ab5bfeb9
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

md5算法过程

MD5以512位为一个分组处理输入，每个分组分成16个32位的子分组，经过处理后，输出四个32位分组，这四个32位分组级联后生成一个128位的MD5值。

一、填充：如果输入信息长度（以bit记）模512不余448，那就要对输入信息进行填充，填充一个1和若干个0，使得信息长度变成512N+448，*若消息长度本身即为448，仍要填充512位，使其长度变成960

二、记录：用64位记录输入信息的长度，然后添加到第一步的信息中，形成（N+1）*512的信息；

三、装入默认值：A=0x01234567,B=0x89ABCDEF,C=0xFEDCBA98,D=0x76543210。这里每个缓存均为32位（16进制四位，八个数）

四、分组：将512一组的数据进行分组，分成16个32位的子分组，将与幻数进行循环运算。

五、循环运算：这里借用一张MD5原理图进行说明

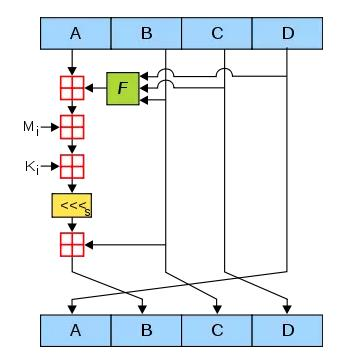
upload successful

MD5分析和魔改

md5的源码，直接github上一搜一大把，就懒得copy了。
上文提到的4个东西

信息分组定义
标准幻数定义
常量表T
辅助方法

这四个东西都可以作为md5的特征，看看findcrypt这个插件，在ida中是如何识别md5算法的。

https://github.com/polymorf/findcrypt-yara/blob/master/findcrypt3.rules

rule MD5_Constants {
	meta:
		author = "phoul (@phoul)"
		description = "Look for MD5 constants"
		date = "2014-01"
		version = "0.2"
	strings:
		// Init constants
		$c0 = { 67452301 }
		$c1 = { efcdab89 }
		$c2 = { 98badcfe }
		$c3 = { 10325476 }
		$c4 = { 01234567 }
		$c5 = { 89ABCDEF }
		$c6 = { FEDCBA98 }
		$c7 = { 76543210 }
		// Round 2
		$c8 = { F4D50d87 }
		$c9 = { 78A46AD7 }
	condition:
		5 of them
}

rule MD5_API {
	meta:
		author = "_pusher_"
		description = "Looks for MD5 API"
		date = "2016-07"
	strings:
		$advapi32 = "advapi32.dll" wide ascii nocase
		$cryptdll = "cryptdll.dll" wide ascii nocase
		$MD5Init = "MD5Init" wide ascii
		$MD5Update = "MD5Update" wide ascii
		$MD5Final = "MD5Final" wide ascii
	condition:
		($advapi32 or $cryptdll) and ($MD5Init and $MD5Update and $MD5Final)
}

用标准幻数来识别的。

试着想想，在客户端暴露md5，或者直接在java层调用api的话，那么其实用任何语言的算法都能够实现。

此时又带来算法泄露的问题，有些大厂是把md5修改之后，直接编译器给vm了。这样在c层分析起来也特别困难。

md5修改点

以上说的4处特征，都可以修改。

信息分组定义：每次填充的值都是标准幻数，我们可以把16个字节的幻数，填充成每次md5加密之后的结果。
标准幻数定义：这是按照小端序来排列的，可以直接换成大端序。
常量表T：T是一个常量表，T[i] = 4294967296 * abs(sin(i))的运算结果取整，其中i=1…64，
				sin函数可以直接替换成cos函数。
辅助方法：F,G,H,I 的算法依旧可以自己骚味修改修改。
最后建议如果客户端的话，放在ndk或者dylib动态链接库中。

AES

讲完了hash算法(不可逆)，来讲讲对称算法aes的作用。

这套算法在工作中也经常用，用来加密一些敏感信息….

基本 AES 加密

AES 算法会将纯文本字符串分解为 16 字节的“块”，这些“块”会经过几轮加密。这些步骤在官方AES 文档中有详细说明：

展开提供的密钥（密钥扩展[部分）
使用扩展密钥的明文块上的AddRoundKey函数
多轮加密
1. 块上的SubBytes功能
2. 块上的ShiftRows功能
3. 块上的MixColumns功能
4. AddRoundKey 函数
最终SubBytes调用
最后的 ShiftRows 调用
最后的 AddRoundKey 调用

使用的轮数和扩展密钥EK的大小取决于所提供密钥的大小。下表显示了密钥长度、轮数和扩展密钥长度之间的相关性：

Key Length (Bits)	Number of Rounds	Expanded Key Length (Words)
128	10	44
192	12	72
256	14	112

也就是所谓的aes的key的长度，对应的轮数。

key：16位加密轮数 10轮

key：24位加密轮数 12轮

key：32位加密轮数 14轮

AES加密流程

def cipher(self, pt):
      """Basic AES implementation.

      Args:
          pt (bytes): Plaintext to encrypt

      Returns:
          list: Encrypted Ciphertext formatted as list of bytes
      """
      state = self.rows_to_columns(pt)
      self.add_round_key(state, self.ek[0:4]) #ek is the expanded key
      for round in range(1, 10):
          self.sub_bytes(state)
          self.shift_rows(state)
          self.mix_columns(state)
          self.add_round_key(state, self.ek[round*4:(round*4)+4])
      self.sub_bytes(state)
      self.shift_rows(state)
      self.add_round_key(state, self.ek[-4:])
      return state

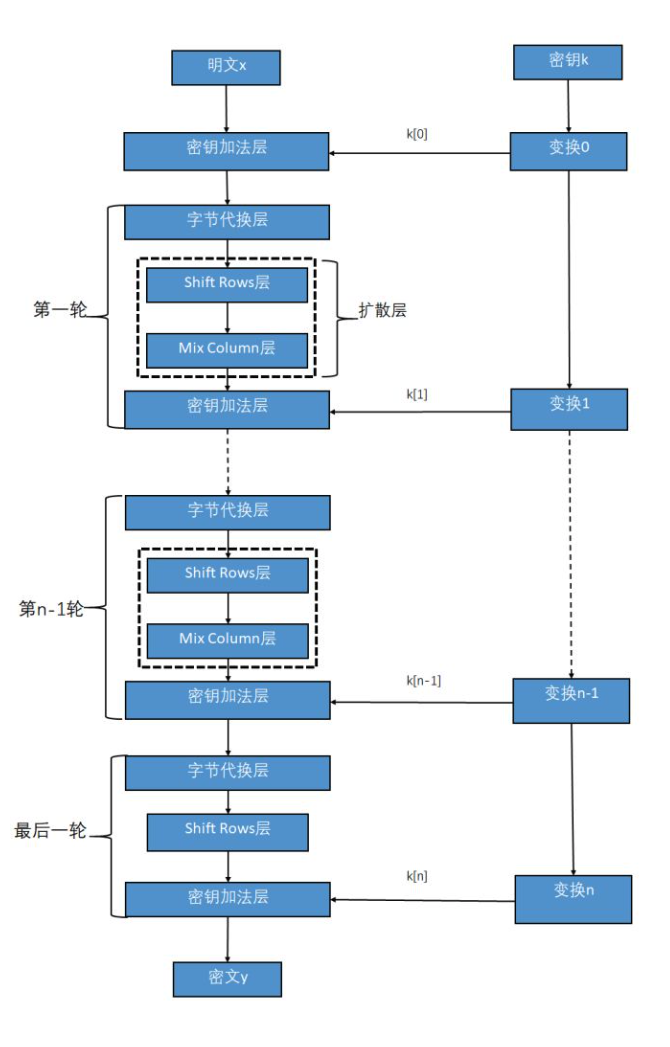
upload successful

从这张流程图开始分析。原理就不过多坦述，具体可以看看wiki上的介绍。现在只是加强一下算法特征的认识，

后续逆向过程中，或者开发过程中，好针对性的做出相应措施。

在AES中，每一个状态都会被列为一个4x4的矩阵，也就是明文，密钥等都会被映射到4X4的矩阵中。

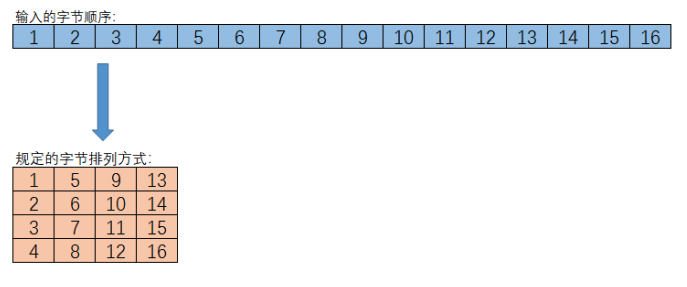
upload successful

如果长度超出，就会无限往右扩展。。。。

上代码：

void AES::EncryptBlock(const unsigned char in[], unsigned char out[],
                       unsigned char *roundKeys) {
  unsigned char **state = new unsigned char *[4];
  state[0] = new unsigned char[4 * Nb];
  int i, j, round;
  for (i = 0; i < 4; i++) {
    state[i] = state[0] + Nb * i;
  }

  for (i = 0; i < 4; i++) {
    for (j = 0; j < Nb; j++) {
      state[i][j] = in[i + 4 * j];
    }
  }

  AddRoundKey(state, roundKeys);

  for (round = 1; round <= Nr - 1; round++) {
    SubBytes(state);
    ShiftRows(state);
    MixColumns(state);
    AddRoundKey(state, roundKeys + round * 4 * Nb);
  }

  SubBytes(state);
  ShiftRows(state);
  AddRoundKey(state, roundKeys + Nr * 4 * Nb);

  for (i = 0; i < 4; i++) {
    for (j = 0; j < Nb; j++) {
      out[i + 4 * j] = state[i][j];
    }
  }

  delete[] state[0];
  delete[] state;
}

首先第一步就要对密钥K进行变换扩展。

AES 的扩展密钥是从原始密钥派生的四字节字的列表。数组中的第一个单词与原始键相同。例如，键数组中的前四个字节将是扩展键中的第一个单词，EK，如下所示：

key = [0x00, 0x11, 0x22, 0x33, 0x44, 0x55, 0x66, 0x77, 0x88, 0x99, 0xaa, 0xbb, 0xcc, 0xdd, 0xee, 0xff]

expanded_key = [0x00112233,
                0x44556677,
                0x8899aabb,
                0xccddeeff,
                ...]

upload successful

void AES::AddRoundKey(unsigned char **state, unsigned char *key) {
  int i, j;
  for (i = 0; i < 4; i++) {
    for (j = 0; j < Nb; j++) {
      state[i][j] = state[i][j] ^ key[i + 4 * j];
    }
  }
}

进行n-1轮的循环加密

subbytes，字节代换，字节代换层的主要功能就是让输入的数据通过S_box表完成从一个字节到另一个字节的映射，这里的S_box表是通过某种方法计算出来的，具体的计算方法就不介绍了比较复杂，我们基础部分就只给出计算好的S_box结果。

0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0x63	0x7C	0x77	0x7B	0xF2	0x6B	0x6F	0xC5	0x30	0x01	0x67	0x2B	0xFE	0xD7	0xAB	0x76
0xCA	0x82	0xC9	0x7D	0xFA	0x59	0x47	0xF0	0xAD	0xD4	0xA2	0xAF	0x9C	0xA4	0x72	0xC0
0xB7	0xFD	0x93	0x26	0x36	0x3F	0xF7	0xCC	0x34	0xA5	0xE5	0xF1	0x71	0xD8	0x31	0x15
0x04	0xC7	0x23	0xC3	0x18	0x96	0x05	0x9A	0x07	0x12	0x80	0xE2	0xEB	0x27	0xB2	0x75
0x09	0x83	0x2C	0x1A	0x1B	0x6E	0x5A	0xA0	0x52	0x3B	0xD6	0xB3	0x29	0xE3	0x2F	0x84
0x53	0xD1	0x00	0xED	0x20	0xFC	0xB1	0x5B	0x6A	0xCB	0xBE	0x39	0x4A	0x4C	0x58	0xCF
0xD0	0xEF	0xAA	0xFB	0x43	0x4D	0x33	0x85	0x45	0xF9	0x02	0x7F	0x50	0x3C	0x9F	0xA8
0x51	0xA3	0x40	0x8F	0x92	0x9D	0x38	0xF5	0xBC	0xB6	0xDA	0x21	0x10	0xFF	0xF3	0xD2
0xCD	0x0C	0x13	0xEC	0x5F	0x97	0x44	0x17	0xC4	0xA7	0x7E	0x3D	0x64	0x5D	0x19	0x73
0x60	0x81	0x4F	0xDC	0x22	0x2A	0x90	0x88	0x46	0xEE	0xB8	0x14	0xDE	0x5E	0x0B	0xDB
0xE0	0x32	0x3A	0x0A	0x49	0x06	0x24	0x5C	0xC2	0xD3	0xAC	0x62	0x91	0x95	0xE4	0x79
0xE7	0xC8	0x37	0x6D	0x8D	0xD5	0x4E	0xA9	0x6C	0x56	0xF4	0xEA	0x65	0x7A	0xAE	0x08
0xBA	0x78	0x25	0x2E	0x1C	0xA6	0xB4	0xC6	0xE8	0xDD	0x74	0x1F	0x4B	0xBD	0x8B	0x8A
0x70	0x3E	0xB5	0x66	0x48	0x03	0xF6	0x0E	0x61	0x35	0x57	0xB9	0x86	0xC1	0x1D	0x9E
0xE1	0xF8	0x98	0x11	0x69	0xD9	0x8E	0x94	0x9B	0x1E	0x87	0xE9	0xCE	0x55	0x28	0xDF
0x8C	0xA1	0x89	0x0D	0xBF	0xE6	0x42	0x68	0x41	0x99	0x2D	0x0F	0xB0	0x54	0xBB	0x16

逆SBOX自己github找找就行。

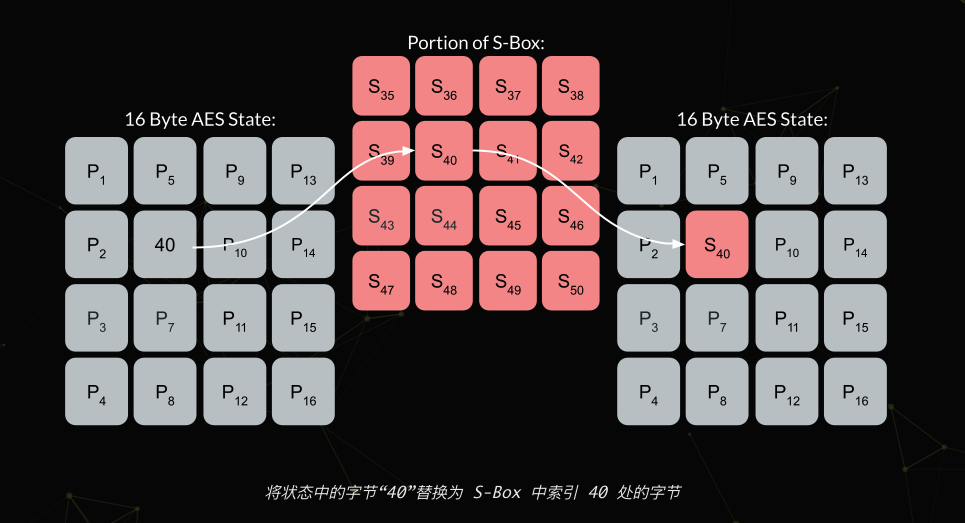
upload successful

void AES::SubBytes(unsigned char **state) {
  int i, j;
  unsigned char t;
  for (i = 0; i < 4; i++) {
    for (j = 0; j < Nb; j++) {
      t = state[i][j];
      state[i][j] = sbox[t / 16][t % 16];
    }
  }
}

ShiftRows行位移，行位移操作最为简单，它是用来将输入数据作为一个4·4的字节矩阵进行处理的，然后将这个矩阵的字节进行位置上的置换。ShiftRows子层属于AES手动的扩散层，目的是将单个位上的变换扩散到影响整个状态当，从而达到雪崩效应。在加密时行位移处理与解密时的处理相反，我们这里将解密时的处理称作逆行位移。它之所以称作行位移，是因为它只在4·4矩阵的行间进行操作，每行4字节的数据。在加密时，保持矩阵的第一行不变，第二行向左移动8Bit(一个字节)、第三行向左移动2个字节、第四行向左移动3个字节。而在解密时恰恰相反，依然保持第一行不变，将第二行向右移动一个字节、第三行右移2个字节、第四行右移3个字节。操作结束！

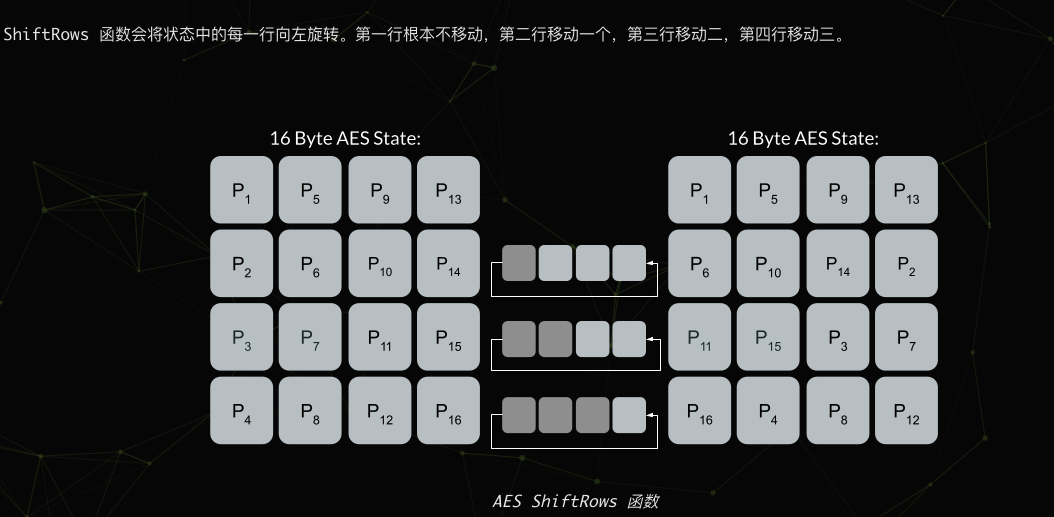
upload successful

void AES::ShiftRow(unsigned char **state, int i,
                   int n)  // shift row i on n positions
{
  unsigned char *tmp = new unsigned char[Nb];
  for (int j = 0; j < Nb; j++) {
    tmp[j] = state[i][(j + n) % Nb];
  }
  memcpy(state[i], tmp, Nb * sizeof(unsigned char));

  delete[] tmp;
}

void AES::ShiftRows(unsigned char **state) {
  ShiftRow(state, 1, 1);
  ShiftRow(state, 2, 2);
  ShiftRow(state, 3, 3);
}

Mixcolums列混淆,MixColumns 将对状态中的每一列执行矩阵乘法。这里的乘法也像 Key Expansion 函数一样使用伽罗瓦域。我设法从用户 lovasoa的 GitHub 中找到了该算法的纯 Python 实现，如下所示：

def gmul(a, b):
    """Special AES function used for multiplication

    Args:
        a (int): Integer to multiply
        b (int): Integer to multiply

    Returns:
        int: The product of the values
    """
    p = 0
    for c in range(8):
        if b & 1:
            p ^= a
        a <<= 1
        if a & 0x100:
            a ^= 0x11b
        b >>= 1
    return p

矩阵乘法如下所示：

整个函数可以显示为以下 Python 代码：

def mix_columns(self, state):
      """AES MixColumns Method.

      Args:
          state (list): AES State
      """
      for i in range(4):
          a = state[i]
          b = state[i+4]
          c = state[i+8]
          d = state[i+12]
          state[i] = gmul(2, a) ^ gmul(3, b) ^ c ^ d
          state[i+4] = a ^ gmul(2, b) ^ gmul(3, c) ^ d
          state[i+8] = a ^ b ^ gmul(2, c) ^ gmul(3, d)
          state[i+12] = gmul(3, a) ^ b ^ c ^ gmul(2, d)

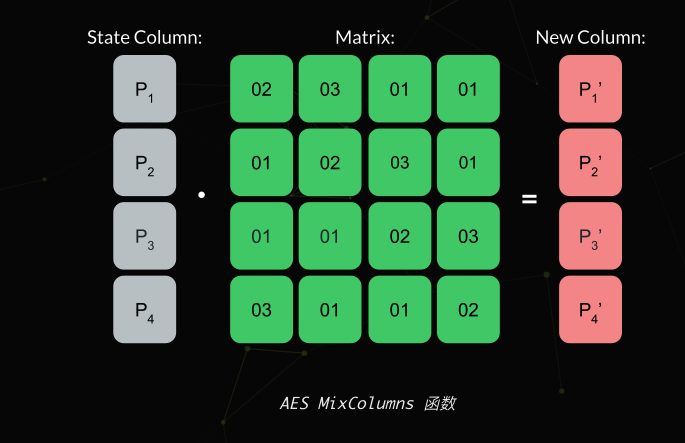
upload successful

void AES::MixColumns(unsigned char **state) {
  unsigned char temp_state[4][4];

  for (size_t i = 0; i < 4; ++i) {
    memset(temp_state[i], 0, 4);
  }

  for (size_t i = 0; i < 4; ++i) {
    for (size_t k = 0; k < 4; ++k) {
      for (size_t j = 0; j < 4; ++j) {
        if (CMDS[i][k] == 1)
          temp_state[i][j] ^= state[k][j];
        else
          temp_state[i][j] ^= GF_MUL_TABLE[CMDS[i][k]][state[k][j]];
      }
    }
  }

  for (size_t i = 0; i < 4; ++i) {
    memcpy(state[i], temp_state[i], 4);
  }
}

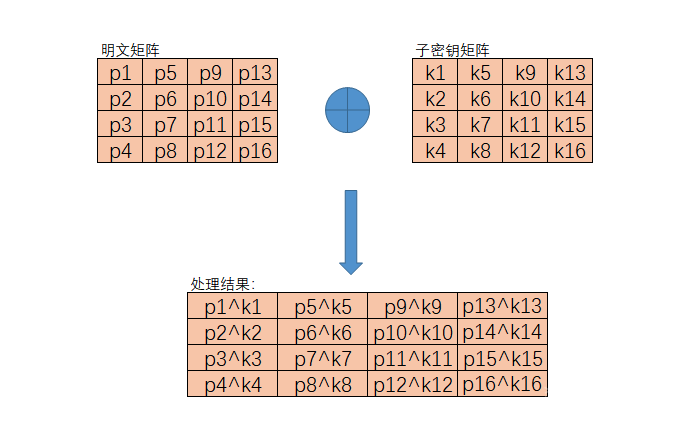
AddRoundKey加固键，AES 中的 AddRoundKey 函数将通过状态的每一列对扩展密钥的一部分进行异或。

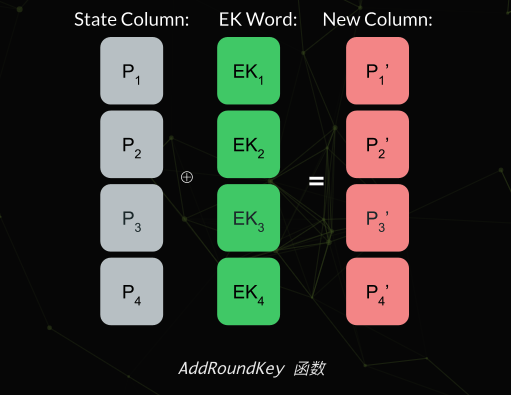
upload successful

最后一轮：

1
2
3

SubBytes(state);
ShiftRows(state);
AddRoundKey(state, roundKeys + Nr * 4 * Nb);

AEST表

这个表示干嘛的呢，一张图显示。

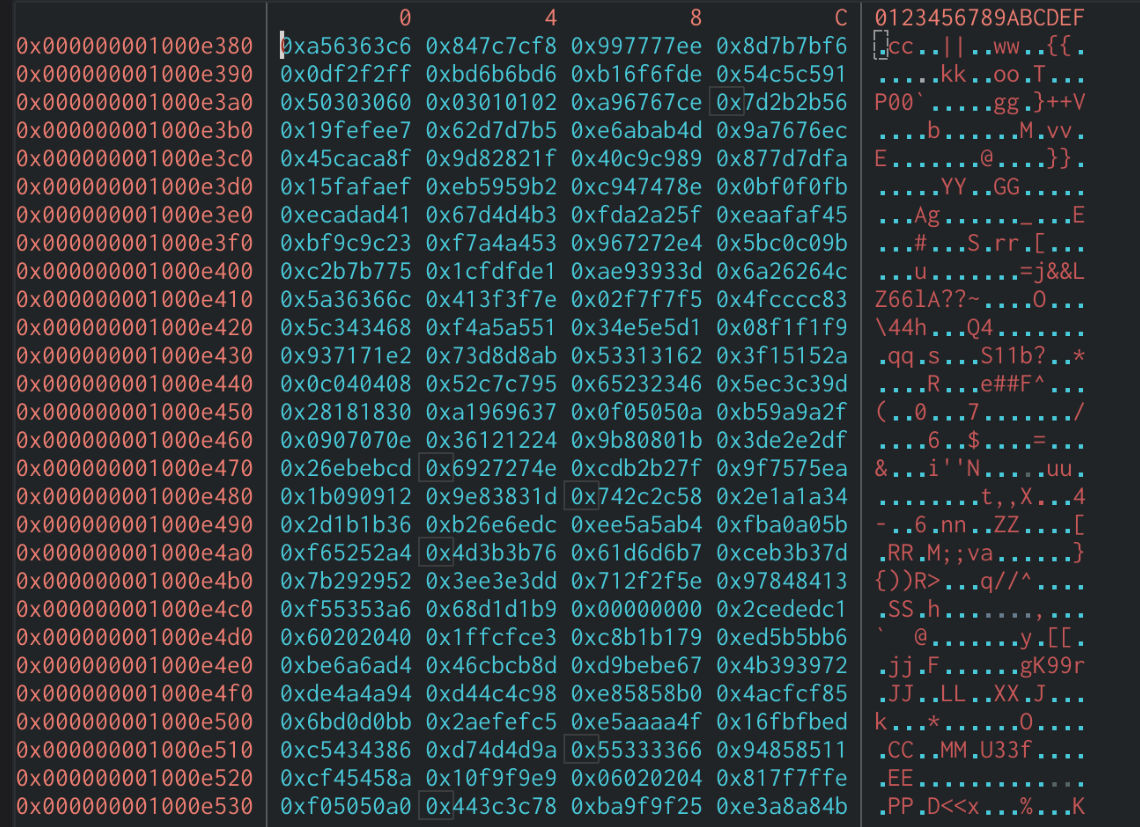
upload successful

有时候在逆向的时候，往往会出现很多这样的表，一般都是5张左右，都是sbox生成的加速表，用来加速aes加解密计算的。

AES 查找表 (T-Table) 方法

为了提高 AES 算法的效率，MixColumns、ShiftRows 和 SubBytes 函数被组合成一个使用五个查找表的操作。密钥扩展算法与原始 AES 算法相同，状态被视为普通数组而不是 4x4 矩阵。

查找表生成

前四个查找表 (T-Tables) 是通过将 S-Box 的每个字节乘以 MixColumns 函数中使用的矩阵来生成的。这将创建四个包含 256 个四字节字的表。它们可以使用以下算法生成：

T1 = {S[i] * 2, S[i], S[i], S[i] * 3}
T2 = {S[i] * 3, S[i] * 2, S[i], S[i]}
T3 = {S[i], S[i] *  3, S[i] * 2, S[i]}
T4 = {S[i], S[i], S[i] * 3, S[i] * 2}

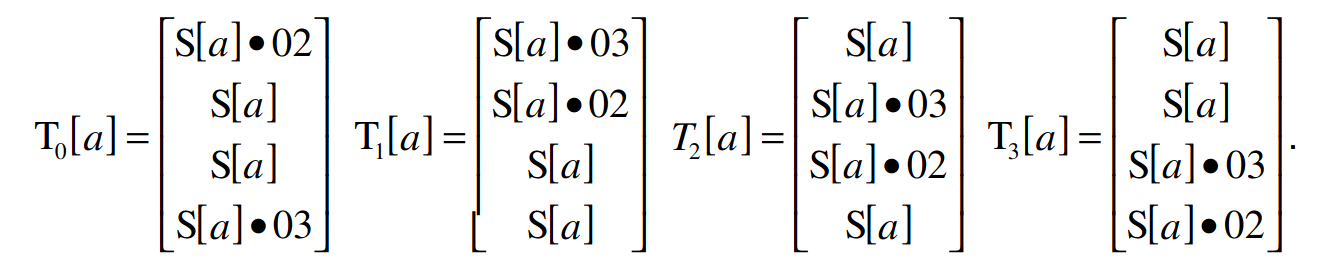
upload successful

最终的 T-Table 将 S-Box 的每个字节组合成一个四字节的字，并且仅在最后一轮加密期间使用。

1 2	# Final T-Table generation T5 = {S[i], S[i], S[i], S[i]}

查找表的整个生成过程可能类似于以下 Python 代码：

def generate_t_tables(self):
    """Generates the tables used for the AES lookup table method."""
    self.t1 = []
    self.t2 = []
    self.t3 = []
    self.t4 = []
    self.t5 = []
    for i in range(len(self.SBOX)):
        word1 = [gmul(self.SBOX[i], 2), self.SBOX[i],
                 self.SBOX[i], gmul(self.SBOX[i], 3)]
        word2 = [gmul(self.SBOX[i], 3), gmul(self.SBOX[i], 2),
                 self.SBOX[i], self.SBOX[i]]
        word3 = [self.SBOX[i], gmul(self.SBOX[i], 3),
                 gmul(self.SBOX[i], 2), self.SBOX[i]]
        word4 = [self.SBOX[i], self.SBOX[i],
                 gmul(self.SBOX[i], 3), gmul(self.SBOX[i], 2)]
        word5 = [self.SBOX[i]] * 4
        self.t1.append(struct.unpack('>I', bytes(word1))[0])
        self.t2.append(struct.unpack('>I', bytes(word2))[0])
        self.t3.append(struct.unpack('>I', bytes(word3))[0])
        self.t4.append(struct.unpack('>I', bytes(word4))[0])
        self.t5.append(struct.unpack('>I', bytes(word5))[0])

回合加密

对于每一轮加密，AES T-Table 算法将对原始明文数组索引处的四个查找表的一个字节进行异或。例如，一个普通的回合看起来像下面的伪代码：

A[0] = PT[0:4] ^ W[0]
A[1] = PT[4:8] ^ W[1]
A[2] = PT[8:12] ^ W[2]
A[3] = PT[12:16] ^ W[3]

K = 4

for round in NUM_ROUNDS:
  S[0:4] = A[0] # Convert word to bytes
  S[4:8] = A[1]
  S[8:12] = A[2]
  S[12:16] = A[3]
  A[0] = T1[S[0]] ^ T2[S[5]] ^ T3[S[10]] ^ T4[S[15]] ^ W[K+0]
  A[1] = T1[S[4]] ^ T2[S[9]] ^ T3[S[14]] ^ T4[S[3]] ^ W[K+1]
  A[2] = T1[S[8]] ^ T2[S[13]] ^ T3[S[2]] ^ T4[S[7]] ^ W[K+2]
  A[3] = T1[S[12]] ^ T2[S[1]] ^ T3[S[6]] ^ T4[S[11]] ^ W[K+3]

此方法比调用单独的 SubBytes、ShiftRows 和 MixColumns 函数更有效，因为它是一步完成的。一次组合所有方法时，无需执行多个循环或函数调用。

最后一轮

最后一轮加密类似于普通轮，除了它使用第五个 T-Table 并且每个 XOR 都附加到密文中。下面的伪代码演示了这个过程：

CT[0:4] = T5[S[0]] ^ T5[S[5]] ^ T5[S[10]] ^ T5[S[15]] ^ W[K+0]
CT[4:8] = T5[S[4]] ^ T5[S[9]] ^ T5[S[14]] ^ T5[S[3]] ^ W[K+1]
CT[8:12] = T5[S[8]] ^ T5[S[13]] ^ T5[S[2]] ^ T5[S[7]] ^ W[K+2]
CT[12:16] = T5[S[12]] ^ T5[S[1]] ^ T5[S[6]] ^ T5[S[11]] ^ W[K+3]

AES T 表 Python 代码

AES T-Table 实现的完整代码如下所示：

def cipher_t_table(self, pt):
    """Lookup Table AES implementation.

    Args:
        pt (bytes): Plaintext to encrypt

    Returns:
        bytes: Encrypted Ciphertext
    """
    ct = []
    a = [0, 0, 0, 0]
    # t is a temporary array to avoid us changing array a while performing the algorithm
    t = [0, 0, 0, 0]
    a[0] = struct.unpack('>I', pt[0:4])[0] ^ self.ek[0]
    a[1] = struct.unpack('>I', pt[4:8])[0] ^ self.ek[1]
    a[2] = struct.unpack('>I', pt[8:12])[0] ^ self.ek[2]
    a[3] = struct.unpack('>I', pt[12:16])[0] ^ self.ek[3]
    print(a)
    for round in range(1, 10):
        for i in range(4):
            # Using binary rotation instead of splitting words into array
            t[i] = (self.t1[(a[i] >> 24) & 0xff] ^
                    self.t2[(a[(i + 1) % 4] >> 16) & 0xff] ^
                    self.t3[(a[(i + 2) % 4] >> 8) & 0xff] ^
                    self.t4[(a[(i + 3) % 4]) & 0xff] ^
                    self.ek[(round*4)+i])
        a = t.copy()

    # Final round of encryption
    for i in range(4):
        ct.append(self.SBOX[(a[i] >> 24) & 0xff] ^
                  ((self.ek[-4+i] >> 24) & 0xff))
        ct.append(self.SBOX[(a[(i + 1) % 4] >> 16) & 0xff] ^
                  ((self.ek[-4+i] >> 16) & 0xff))
        ct.append(self.SBOX[(a[(i + 2) % 4] >> 8) & 0xff] ^
                  ((self.ek[-4+i] >> 8) & 0xff))
        ct.append(self.SBOX[(a[(i + 3) % 4]) & 0xff] ^
                  ((self.ek[-4+i]) & 0xff))
    return bytes(ct)

AES分析和魔改

参考：https://github.com/SergeyBel/AES/blob/master/src/AES.cpp

写了个ndk的demo，逆向分析一下在so层里面的逻辑。

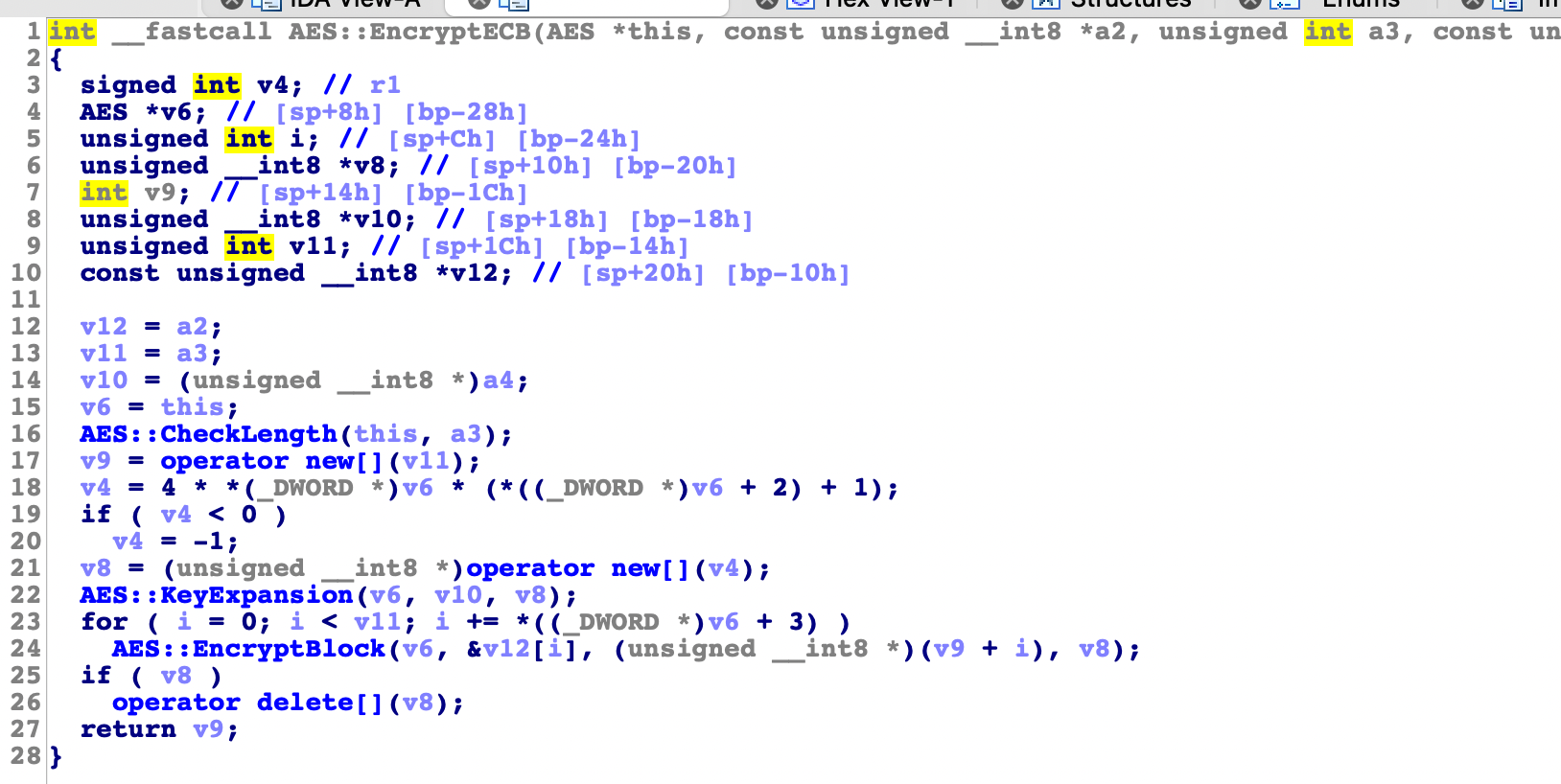
upload successful
这是ida解析的伪代码。

对于我们要在实际逆向应用中，快速定位，一般都是会把这些符号表去掉的，没有那个蠢逼会傻傻的把函数名给你看。

借助ida的findcrypt插件，一键识别位置。

upload successful

搜寻不到的时候，盯着sbox表，用010搜索特征值，比如0x63,0x7c等等….

.text:000108B6 loc_108B6                               ; CODE XREF: AES::SubBytes(uchar **)+28↑j
.text:000108B6                 LDR             R0, [SP,#0x18+var_8]
.text:000108B8                 LDR             R1, [SP,#0x18+var_C]
.text:000108BA                 LDR.W           R0, [R0,R1,LSL#2]
.text:000108BE                 LDR             R1, [SP,#0x18+var_10]
.text:000108C0                 LDRB            R0, [R0,R1]
.text:000108C2                 STRB.W          R0, [SP,#0x18+var_11]
.text:000108C6                 LDRB.W          R0, [SP,#0x18+var_11]
.text:000108CA                 AND.W           R1, R0, #0xF0
.text:000108CE                 LDR             R2, =(RijnDael_AES_LONG_2518C - 0x108D4)
.text:000108D0                 ADD             R2, PC  ; RijnDael_AES_LONG_2518C  sbox表
.text:000108D2                 ADD             R1, R2
.text:000108D4                 AND.W           R0, R0, #0xF
.text:000108D8                 LDRB            R0, [R1,R0]
.text:000108DA                 LDR             R1, [SP,#0x18+var_8]
.text:000108DC                 LDR             R2, [SP,#0x18+var_C]
.text:000108DE                 LDR.W           R1, [R1,R2,LSL#2]
.text:000108E2                 LDR             R2, [SP,#0x18+var_10]
.text:000108E4                 STRB            R0, [R1,R2]
.text:000108E6                 B               loc_108E8
.text:000108E8 ; ---------------------------------------------------------------------------

搜索aes的key，一般来说aes的key是最重要的。那么首先找到密钥扩展这个地方，因为传参一定有key。后续分析别的app时，会详细讲讲，这里先说说思路。一般拿捏不定，可以trace(埋坑，后续讲)。

addroundkey时，会将明文和key进行异或

.text:00010858 ; ---------------------------------------------------------------------------
.text:00010858
.text:00010858 loc_10858                               ; CODE XREF: AES::AddRoundKey(uchar **,uchar *)+2A↑j
.text:00010858                 LDR             R0, [SP,#0x18+var_8]
.text:0001085A                 LDR             R1, [SP,#0x18+var_10]
.text:0001085C                 LDR.W           R0, [R0,R1,LSL#2]
.text:00010860                 LDR             R2, [SP,#0x18+var_14]
.text:00010862                 LDRB            R3, [R0,R2]
.text:00010864                 LDR.W           R12, [SP,#0x18+var_C]
.text:00010868                 ADD.W           R1, R1, R2,LSL#2
.text:0001086C                 LDRB.W          R1, [R12,R1]
.text:00010870                 EORS            R1, R3  这里汇编指令^
.text:00010872                 STRB            R1, [R0,R2]
.text:00010874                 B               loc_10876
.text:00010876 ; ---------------------------------------------------------------------------

mixcolums列混合时，几个关键的常量：0x02, 0x01, 0x01, 0x03

.text:00010A18 ; ---------------------------------------------------------------------------
.text:00010A18
.text:00010A18 loc_10A18                               ; CODE XREF: AES::MixColumns(uchar **)+B0↑j
.text:00010A18                 LDR             R0, [SP,#0x70+var_5C]
.text:00010A1A                 LDR             R1, =(byte_2528C - 0x10A20)
.text:00010A1C                 ADD             R1, PC  ; byte_2528C
.text:00010A1E                 ADD.W           R1, R1, R0,LSL#2
.text:00010A22                 LDR             R2, [SP,#0x70+var_60]
.text:00010A24                 LDRB            R1, [R1,R2]
.text:00010A26                 LDR             R3, =(byte_2529C - 0x10A2C)
.text:00010A28                 ADD             R3, PC  ; byte_2529C
.text:00010A2A                 ADD.W           R1, R3, R1,LSL#8
.text:00010A2E                 LDR             R3, [SP,#0x70+var_54]
.text:00010A30                 LDR.W           R2, [R3,R2,LSL#2]
.text:00010A34                 LDR             R3, [SP,#0x70+var_64]
.text:00010A36                 LDRB            R2, [R2,R3]
.text:00010A38                 LDRB            R1, [R1,R2]
.text:00010A3A                 ADD             R2, SP, #0x70+var_1C
.text:00010A3C                 ADD.W           R0, R2, R0,LSL#2
.text:00010A40                 LDRB            R2, [R0,R3]
.text:00010A42                 EORS            R1, R2
.text:00010A44                 STRB            R1, [R0,R3]
.text:00010A46                 B               loc_10A48
.text:00010A48 ; ---------------------------------------------------------------------------

参考：

TeslaCrypt勒索软件中的AES算法识别：https://cloud.tencent.com/developer/article/1040293

aes在cutter中识别：https://www.goggleheadedhacker.com/blog/post/reversing-crypto-functions-aes#key-expansion

上面说到的几个点，aes魔改起来，就有太多地方了，但是现在cpu都对aes有加速处理，故此修改一些常量是最简单的。亦如RCON，密钥扩展函数运算等等。

如果不考虑算法被攻破的可能性，可缩减n-1的轮数。

但如果对自己的程序不自信的话，这个时候可以牺牲点性能，采取白盒aes加密的方法，这套强度特别高。

后续放分析过程…

通用加密算法解析和魔改

MD5

散列函数

MD5算法原理

1.填充信息

2.信息处理

md5算法过程

MD5分析和魔改

md5修改点

AES

基本 AES 加密

AES加密流程

AEST表

AES 查找表 (T-Table) 方法

查找表生成

回合加密

最后一轮

AES T 表 Python 代码

AES分析和魔改